Naturally-Forming Geological Tessellations in Death Valley and the Sierra Nevadas

Jenny Huang

Abstract

Regular hexagonal tessellations are prevalent and striking formations within nature that have long provoked human wonder. Honeycombs often come to mind as the classic, biological example of these hexagonal tessellations; however, they just as miraculously occur in geological contexts. This paper investigates the mechanism of formation for tessellations in columnar jointing, mud crack networks, and salt pans. While jointed columns and salt pans display regular hexagonal tessellation, mud crack networks more often exhibit varied polygonal or rectilinear tessellations; self-organizing processes of crack healing and reformation can eventually evolve these tessellations such that they become hexagonal. Examples of these landscapes can be found throughout locations in Death Valley and the Sierra Nevada visited by Indiana University’s 2015 Geol-G190 class-namely at Owens River Gorge, Devils Postpile, Badwater Basin, and Devils Golf Course.

Introduction

A tessellation, mathematically defined, is the exact tiling of a two-dimensional plane with geometric shapes such that there exist no overlaps or gaps in the plane; in the cases of the geological tessellations discussed here, cooling and desiccating processes form the regular polygonal tiles. Equilateral triangles, squares, and regular hexagons can all fit together exactly to uniformly tile planes, but the use of regular hexagons is especially favored by nature due to their perimeter-to-area efficiency. Of the three shapes mentioned, regular hexagons maximize the ratio of the area of the hexagon and the length of its perimeter – in other words, hexagons are the most energy-efficient shape to enclose a space, to relieve stress via cracks, et cetera. As energy is the currency of nature, the efficiency and organizedness of regular hexagons make them an attractive pattern for nature to create. In jointed columns and polygonal salt pans, regular hexagonal tessellation is prevalent, whereas in mud crack networks, the tessellations tend to originate with fewer (an average of four) sides per tessellating tile. Even if a mud crack network’s tessellation is not initially hexagonal, though, self-organizing dynamical processes of crack healing and reformation can cause a crack network to evolve from rectilinear to hexagonal.

Mechanisms of initial tessalation formation

Columnar jointing

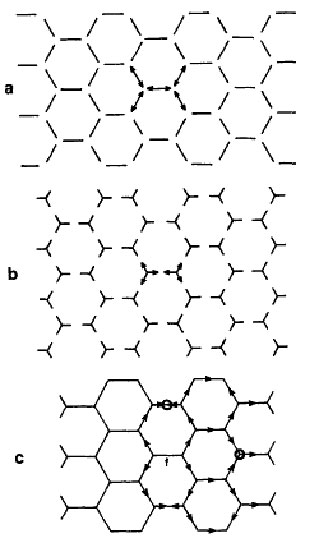
Columnar joints are thermal cracks systems that are oriented perpendicular to the direction of maximum stress [Budkewitsch, 1994]. A hot body of rock – a lava or ash flow, for example – cools from the outside-in such that the solidifying outer part of the rock contracts before the still-hot interior. Consequently, horizontal tensile stresses between the differently-temperatured rock arise; when the thermal contraction stress exceeds the strength of the rock, the rock cracks perpendicular to the isothermal planes [Grossenbacher and McDuffie, 1995; Saliba, 2003]. Sixty- and 120-degree angles of cracking most effectively relieve these thermal stresses; however, 120-degree angles are preferred, as they comprise regular hexagons that efficiently minimize the total crack area while relieving thermal stress [Mallet, 1875; Iddings, 1886]. When the rock material is homogeneous, the contractile forces responsible for these 120-degree cracks exert themselves equally in all directions over the cooling surface, resulting in the centers of contraction being equidistantly placed throughout the cooling rock; this uniformity gives rise to near-perfect hexagonal columns whose cross-sections display regular hexagonal tessellation (see Figure 1) [Iddings, 1886]. The diameter of each column varies inversely with the cooling rate of the lava [Grossenbacher and McDuffie, 1995].

Figure 1. Illustrations of theories for the origin of columnar jointing. In each case, the placement of vertices must be precise in order for regular hexagon formation (Gray, 1986).

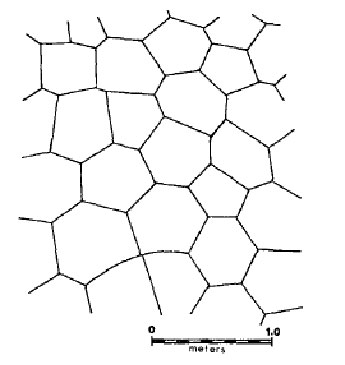
As the material comprising the lava is not perfectly homogenous, though, the distribution and angles of cracking do not uniformly form the ideal case of regular hexagons: while the overall trend for columnar jointing remains hexagonal symmetry, columns with cross-sections of anywhere from three to eight sides are common [Columnar Jointing, 2011]. The molten lava cools from the air-exposed top downwards and more slowly from the ground-contacting bottom upwards, resulting in either two colonnade layers (columns) enclosing an entablature layer of entablature (irregular array) or two colonnade layers meeting imperfectly in the middle [Long and Wood, 1986]. Within the Sierra Nevada mountain range, columnar jointing can be found anywhere from the rhyolitic formations in the Owens River Gorge to the textbook example of tessellated columns at the basaltic Devil’s Postpile (Figure 2).

Figure 2. View of Devils Postpile jointing from the top (Gray et al., 1976).

Mud Cracks

Tessellations in crack patterns of mud require three main "steps" of formation: drying, shrinking, and cracking of the mud. The drying is a result of a thermodynamic imbalance between the moisture of the mud and its surroundings, causing evaporation to desiccate the mud [Peron et al., 2009]. Shrinkage arises from a decrease in liquid pressure and an increase in suction caused by this evaporation, and desiccation cracks form if the shrinkage is constrained (if the mud were allowed to shrink without constraint to its movement, then there would be no reason for it to crack) [Corte and Higashi, 1960]. These constraints responsible for cracking can originate from traction or displacement boundary conditions (e.g. frictional forces), eigenstress concentrations within the desiccated material, or inhomogeneity of composition [Hueckel, 1992]. In hot and dry locations like Death Valley, CA, where rare rainfall leaves ephemeral bodies of water and mud that soon desiccate due to climate, mud crack networks are prevalent.

Figure 3. Mud cracks of a playa in Panamint Valley, Death Valley (Jim Patterson Photography).

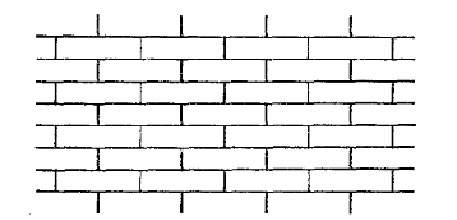
The polygonal fracturing of mud gives rise to crack networks that are much less regularly tessellated than those of columnar joints. While both columnar joint crack networks and mud cracks networks are three-connected – each vertex is shared by three polygons – mud crack tessellations contain many fewer hexagons; in fact, a "tile" of mud has an approximate average of only four sides (see Figure 3) [Gray et al., 1976]. This disparity arises due to the different formations in which the cracks meet one another: whereas cracks in a cross-section of jointed columns meet in a Y-formation, mud cracks truncate each other in a formation that resembles the capital letter T. Figure 4 simplifies and illustrates how T-shaped crack networks, though topologically equivalent to a net of regular hexagons, give rise to quadrilateral tiles [Gray et al., 1976]. T-junctions form as individual cracks nucleate at approximately random nodes and grow in both directions until truncated by another crack. A growing crack is oriented such that it maximally relieves local stress; the largest stresses near an existing fracture are perpendicular to the fracture, resulting in new cracks that truncate the old cracks nearly orthogonally [Gray, 1986].

Figure 4. Illustration of T-shaped junctions and their resulting rectilinear tessalations (Gray et al., 1976).

Topologically, mud crack patterns resemble Gilbert tessellations [Gray et al., 1976]. A tessellation studied in applied mathematics, Gilbert tessellations serve as a mathematical model for random crack network formation – including, relevantly, the formation of mud cracks [Gilbert, 1967]. Gilbert’s model suggests that cracks nucleate at a set of random points across a plane and spread according to a Poisson distribution. Each crack spreads at a uniformly random slope (or, in the case of mud cracks, at the orientation that best relieves stress) in two opposite directions in a line that intersects the initial vertex and stops spreading once it reaches another crack – forming a T-junction, as discussed [Gilbert, 1967].

Saltpans

Precipitated salt pans, which form when a dry climate causes ephemeral bodies of rainwater to evaporate, can also display polygonal tessellations. Where the ephemeral water meets the dry air, it evaporates and leaves a supersaturated brine; the salt, mainly halite, within this brine crystallizes and falls to the bottom of the pool of water to form layers of crust [Goodall et al., 2000]. A polygonal pattern arises from fracturing as a result of volume shrinkage; the cause of this volume shrinkage is disputed, thought to occur either due to thermal contraction or desiccation. Looking at basaltic columns as an analogy, some scholars (e.g. Lachenbruch, 1962 and Tucker, 1981) prefer thermal contraction as an explanation. Comparisons with mud crack tessellations, though, lead other scholars (e.g. Neal et al., 1968) to point to desiccation as the mechanism. Regardless of the origin of the fracturing, though, the growth of efflorescent salt crystals – salt crystals that crystallize onto sediment grains due to the direct evaporation of the brine on the grains – inhibits lateral movement of the salt crust and causes the polygonal edges to dramatically thrust themselves upwards [Goodall et al., 2000]. The formation of both low- and high-relief salt crusts follow this process, with high-relief (>10 cm) crusts occurring from a greater number of repeated cycles of rainfall and precipitation/evaporation [Goodall et al., 2000]. Death Valley, CA, with its hot and dry climate, is an ideal region for polygonal salt pan formation; both low-relief salt pans (in Badwater Basin, see Figure 5) and high-relief salt pans (at Devil’s Golf Course) display expansive, primarily hexagonal salt tessellation.

Figure 5. Low-relief hexagonal salt pans at Badwater Basin, Death Velley (photograph taken by the author).

Crack evolution from T- to Y-Junctions

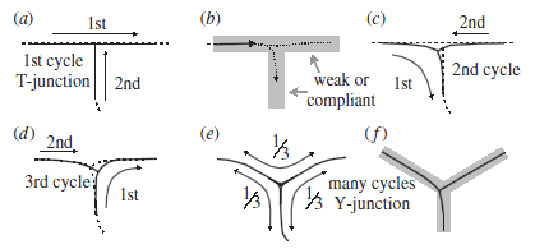
Generally speaking, crack networks are not static geological structures: they can self-organize and continually deform such that T-junctions eventually turn into Y-junctions, and resultingly, rectilinear crack networks become hexagonal. More specifically, the change from a rectilinear to hexagonal tessellation arises when three conditions are met: as defined by Goehring [2013], "(i) that cracks recur or advance repeatedly, (ii) that the previous positions of cracks act as lines of weakness, guiding the next iteration of cracking, and (iii) that the order of opening of cracks may change in each iteration." An evolving crack network implies that the network has some way to change with time – that it is cracking and healing repeatedly. If the crack system retains no "memory" of its previous network, each cycle will result in a new but statistically similar rectilinear tessellation; if the system retains a "memory" of its previous network’s vertices, then the cracks will originate along the same points and also create a statistically similar tessellation; and if the system retains an even stronger "memory," then the tessellation will remain unchanged throughout each cycle [Goehring, 2013]. In order to shift from rectilinear to hexagonal, then, the old cracks must imperfectly direct the formation of the new cracks. Old cracks guide nascent cracks by using energy as their "currency" – for various reasons, following the path of an old crack requires less energy. In some cases, the critical energy release rate is lower proximal to old cracks; in other cases, the strain energy release rate near an old crack is higher; and in other cases, the cracks leave a depression after healing that locally lowers the height of the rock such that the it is energetically favorable for a new crack to form in this depression [Sletten et al., 2003; Goehring, 2013].

Figure 6. Model for the evolution of a rectilinear crack pattern into a hexagonal crack pattern (Goehring, 2013).

The example in Figure 6 illustrates a generalized version of the process of T-shaped junctions become Y-shaped. At first, one crack grows from left to right and another approaches from below to intersect it orthogonally; after healing, a nascent crack following the path of the old crack diverges near the previous vertex due to an asymmetric stress field around the tip of the growing crack. As a result, the crack may progress downwards, and with repeated cycles of cracking and rehealing, the downwards-pointing changes accumulate and lead to a drift from a 90-degree to a 120-degree junction (Figure 7) [Goehring, 2013].

Figure 7. After multiple cycles of cracking and healing, the mud-crack patterns move towards 120-degree-angled Y-junctions (Goehring, 2013).

Conclusion

Polygonal tessellations in geological formations owe their remarkable structure to nature’s desire for energy efficiency: by forming hexagons, rocks can most efficiently release tensional stress associated with cooling and desiccation. In the formation of columnar jointing, thermal contraction of cooling lava produces columns of hexagonal rock that meticulously fit together; in mud crack formation, desiccation creates a less-uniform, rectilinear pattern that may eventually trend towards hexagonal tessellation; and in salt pan formation, repeated rainfall and precipitation/evaporation cause hexagons demarcated by elevated salt ridges to spread across a desert floor. All in all, the idea that tessellation formation is self-organizing – that there is no one governing force that arranges an overall pattern but that, instead, local geological forces work together to form a complex emergent structure of hexagons – serves as a testament to the mathematical and aesthetic elegance of our dynamic physical world.

Works Cited

Budkewitsch, P., and Robin, P.=Y. (1994), Modelling the Evolution of Columnar Joints, Journal of Volcanology and Geothermal Research 59.3, 219-39.

Columnar jointing provides clues to cooling history of lava flows, October 2011, http://hvo.wr.usgs.gov/volcanowatch/view.php?id=94, Hawaii Volcano Observatory, USGS.

Corte, A., and Higashi, A. (1960), Experimental Research on Desiccation Cracks in Soil, U.S. Army Snow and Ice and Permafrost Research Establishment, Research report 66.

Gilbert, E.N. (1967), Random plane networks and needle-shaped crystals, Applications of Undergraduate Mathematics in Engineering, New York: Macmillan.

Goehring, L. (2013), Evolving fracture patterns: columnar joints, mud cracks and polygonal terrain, Philosophical Transactions of the Royal Society A 371.

Gray, N.H, Anderson, J.B., Devine, J.D., and Kwasnik, J. M. (1976), Topological Properties of Random Crack Networks, Mathematical Geology 8.6, 617-626.

Gray, N.H. (1986), Symmetry in a natural fracture pattern: The Origin of Columnar Joint Networks, Computers & Mathematics with Applications 12.3-4, 531-45.

Grossenbacher, K.A. and McDuffie, S.M. (1995), Conductive Cooling of Lava: Columnar Joint Diameter and Stria Width as Functions of Cooling Rate and Thermal Gradient, Journal of Volcanology and Geothermal Research 69.1-2, 95-103.

Hueckel T., (1992) On effective stress concept and deformation in clays subjected to environmental loads: Discussion, Canadian Geotechnical Journal 29, p. 1120-1125.

Iddings, J.P. (1886), Columnar structure in the igneous rocks of Orange Mountain, New Jersey, Am. J. Science 131, 321-330.

Jim Patterson Photography. DEATH-VALLEY-PANAMINT-VALLEY-CRACKED-MUD-SUNSET-01.JPG. Death Valley.M.

Lachenbruch, A.H. (1962), Mechanics of thermal contraction cracks and ice-wedge polygons in permafrost. Geol. Soc. Am. Spec. Paper, 70, New York.

Mallet, R. (1875), Origin and mechanism of production of prismatic (or columnar) structure of basalt, Phil. Mag. 4., 201-226.

Neal, J.T., A.M. Langer, and P.F. Kerr (1968), Giant desiccation polygons of Great Basin playas, Bull. Geol. Soc. Am. 79, 69-90.

Peron, H., Laloui L., Hueckel T., Hu L.B. (2009), Dessication cracking of soils, European Journal of Environmental and Civil Engineering 13.7-8, 869-888.

Saliba, R. and Jagla, E.A. (2003), Analysis of Columnar Joint Patterns from Three-dimensional Stress Modeling, Journal of Geophysical Research 108.B10.

Salt pan tessellations (2015), Badwater Basin, Death Valley, personal photograph by author.

Sletten, R.S., Hallet, B., Fletcher, R.C. (2003), Resurfacing time of terrestrial surfaces by the formation and maturation of polygonal patterned ground, J. Geophys. Res., 108.

Tucker, R.M. (1981), Giant polygons in the Triassic salt of Chesire, England: a thermal contraction model for their origin, J. Sedim. Petrol., 51, 779-786.

 

[Return to Research Projects] [Return to Sierra Home]